[LeetCode] - Two Sum

發表於   |  

Question:
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

此題主要著重在如何有效率的搜尋，這邊使用了三種解法，分別是Brute Force(暴力解)，Binary Search(二分搜尋法)，Hash function(雜湊函數)

假設Hash Function可以達到O(n)的複雜度，那理論上花費時間會是Brute Force > Binary Search > Hash Function，不過實際實驗起來是Brute Force > Binary Search = Hash Function，推測有可能是使用的hash function沒達到O(n)的複雜度，或是LeetCode跑的數據量不足以反應出兩種方式的差距，這部分就不深入探討了

Brute Force

暴力解即是從nums[0]開始往後找是否有數字相加之後可以得到target，如果沒有那就看num[1]接著一樣往後找是否有數字相加之後可以得到target，以此類推，直到找到正確的組合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int* twoSum(int* nums, int numsSize, int target) 
{
	int i, j;
	int *pResult;

	pResult = (int *)malloc(2 * sizeof(int));

	for (i = 0; i < numsSize; i++) {
		for (j = i + 1; j < numsSize; j++) {
			if (*(nums + i) + *(nums + j) == target) {
				*pResult = i;
				*(pResult + 1)= j;
				goto RUN_DONE; 
			}
		}
	}
	RUN_DONE:    
	return pResult;
}

程式就是兩層迴圈，分別兩個兩個相加看是不是要的結果
這裡要注意的是第二層的迴圈在找第二個數字時不用從0開始找，從i+1開始找即可，因為i+1之前的會是已經搜尋過的，例如目前已經搜尋到i = 3那j = 0, 1, 2的狀況分別在之前i = 0 j =3, i = 1 j = 3, i = 2 j = 3時都已經運算過了

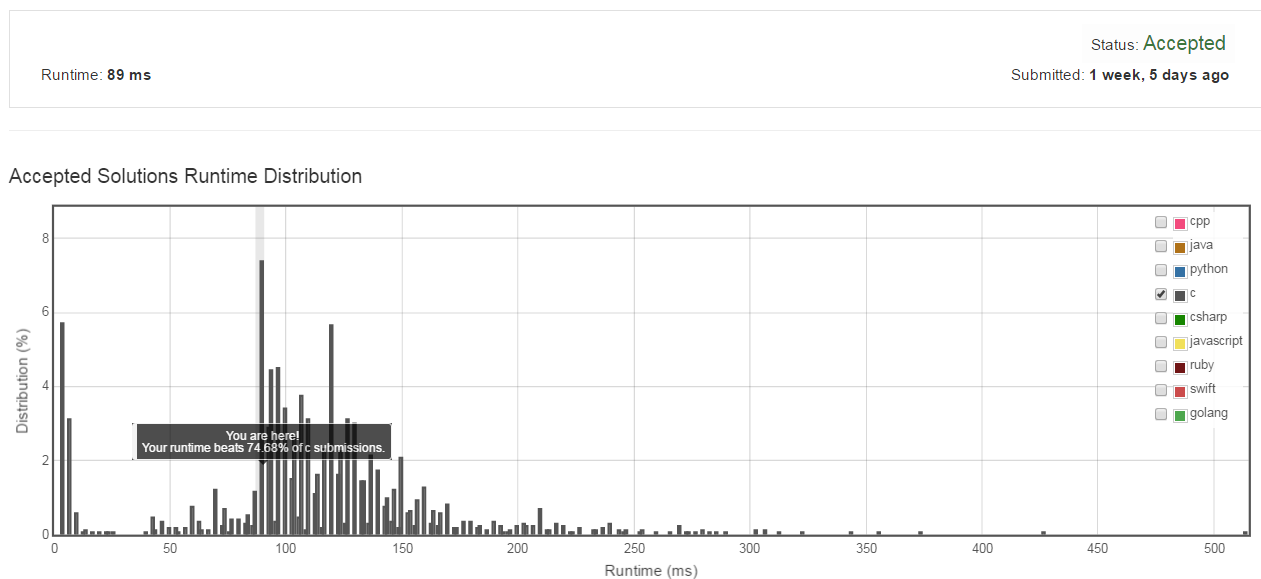
放到leet code上執行的結果為89ms，超過74.68%的上傳程式

二分搜尋法可以將搜尋的複雜度降低成O(logn)，不過需先經過排序，排序方式可以使用standard C有支援的qsort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
int compare(const void *a, const void *b)
{
	return ((*(int *)a - *(int *)b));
}

int binary_search(int *pNums, int size, int val)
{
	int l, u, m;

	l = 0;
	u = size - 1;
	for (;;) {
		if (l > u)
			return -1;
		m = (l + u) >> 1;
		if (*(pNums + m) < val)
			l = m + 1;
		else if (*(pNums + m) == val)
			return m;
		else
			u = m - 1;
    }
}

int* twoSum(int* nums, int numsSize, int target)
{
	int i;
	int offset, val1, val2;
	int *pResult;
	int *pSort_nums;
	int *pCurr_val;
	
	pResult = (int *)malloc(2 * sizeof(int));
	pSort_nums = (int *)malloc(numsSize * sizeof(int));
	memcpy(pSort_nums, nums, sizeof(int) * numsSize);
	//(1)
	qsort(pSort_nums, numsSize, sizeof(int), compare);
	
	pCurr_val = pSort_nums;
	//(2)
	for (i = 0; i < numsSize; i++) {
		val1 = *pCurr_val;
		val2 = target - val1;
		pCurr_val++;
		if (binary_search(pCurr_val, numsSize - i - 1, val2) != -1)
	    	break;
	}
	//(3)
	offset = 0;
	for (i = 0; i < numsSize; i++) {
		if (*(nums + i) == val1 || *(nums + i) == val2) {
			*(pResult + offset) = i;
			if (offset == 1)
				break;
			offset++;
		}
	}

	free(pSort_nums);

	return pResult;
}

(1)首先我們先使用qsort且為由小到大進行排序，因為題目要的答案是數字的位址，而不是數字的值，因此我們不行直接將input的數字串作排序，不然會不知道原本的位址，我們另外令一個一樣大小的陣列，接著memcpy過去，然後將這個陣列作qsort排序

(2)接著一樣找各種配對，不過是使用binary search的方式，而在輸入參數的部分和暴力解一樣，找過的可以不用再找，因此可以看到pCurr_val++且搜尋的大小也可以不斷遞減numsSize - i - 1

(3)最後我們必須從最原始的陣列找出經由binary search找到的兩個數字的位址在哪

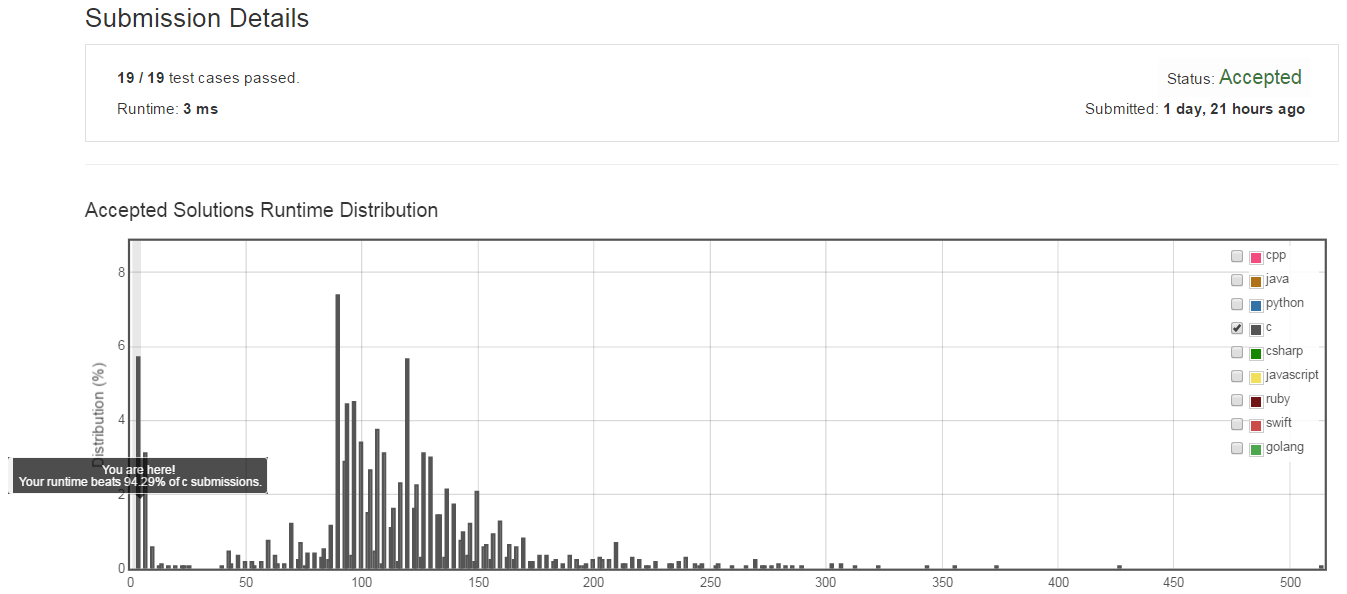
放到leet code上執行的結果為3ms明顯低於暴力解方式，超過94.29%的上傳程式

Hash function

Hash function理想狀況可以將複雜度降至趨近於O(n)，這裡使用的是Paul Hsieh的SuperFastHash，相關src code可自行搜尋，不過這邊的程式碼有經過稍微的修改，因為這裡只需要放置integer，因此改成輸入int，且不用輸入size，並且排除掉非4byte倍數長度的情形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#define HASH_TABLE_NUM 256

unsigned int SuperFastHash (const int val)
{
	unsigned int hash = 0, tmp;
	int rem;
	const char *data = (const char *)&val;

	hash += *(const unsigned short *)data;
	tmp = (*(const unsigned short *)(data + 2) << 11) ^ hash;
	hash = (hash << 16) ^ tmp;
	data += sizeof (unsigned short) << 1;
	hash += hash >> 11;

	/* Force "avalanching" of final 127 bits */
	hash ^= hash << 3;
	hash += hash >> 5;
	hash ^= hash << 4;
	hash += hash >> 17;
	hash ^= hash << 25;
	hash += hash >> 6;

	return hash;
}

int* twoSum(int* nums, int numsSize, int target) 
{
	int i, j, tag = 0;
	int offset, val1, val2;
	int *pResult;
	int (*pHash_table)[HASH_TABLE_NUM];
	int sum[HASH_TABLE_NUM] = {0};
	unsigned int out;
	//(1)
	pResult = (int *)malloc(2 * sizeof(int));
	pHash_table = (int (*)[HASH_TABLE_NUM])malloc(HASH_TABLE_NUM * numsSize * sizeof(int));
	//(2)
	for (i = 0; i < numsSize; i++) {
		out = SuperFastHash(*(const int *)(nums + i));
 		out &= (HASH_TABLE_NUM - 1);
 		(*(pHash_table + sum[out]))[out] = *(nums + i);
		sum[out]++;
	}
	//(3)
	for (i = 0; i < numsSize; i++) {
		val1 = *(nums + i);
		val2 = target - val1;
		out = SuperFastHash((const int)val2);
	 	out &= (HASH_TABLE_NUM - 1);
	 	for (j = 0; j < sum[out]; j++) {
	 		if ((*(pHash_table + j))[out] == val2) {
	 			if (val1 == val2) {
	 				if (tag == 0) {
						tag = 1;
						continue;
					}
				}
				goto RUN_DONE;
			}
		}
	}
	//(4)
RUN_DONE:
	offset = 0;
	for (i = 0; i < numsSize; i++) {
		if (*(nums + i) == val1 || *(nums + i) == val2) {
			*(pResult + offset) = i;
			if (offset == 1)
				break;
			offset++;
		}
	}
	
	free(pHash_table);

	return pResult;
}

(1)pHash_table挖了一塊HASH_TABLE_NUM(256) * numsize的陣列作為hash table使用，使用了256個index來存數字，當然這塊記憶體可能會浪費掉很多空間，不過至少足以保證所有的數字都可以裝的進去，在不考慮記憶體使用空間情況下，可以直接這樣用

(2)接著我們將數字經過hash function運算之後放進hash table裡面，另外使用sum來記錄每個hash table的index裡面放了幾個數字

(3)再來使用hash function來找尋是否有需要的兩個值，這裡要對一個情況作額外的處理，如果有一個target = 6且答案為3+3的狀況，這時我們在hash table找值時必須找到兩次3才算真的符合，因為當你固定其中一個3要去找另外一個3時，會從hash table先找到自己的3，如果找不到另一個3就代表輸入的數列只有一個3

(4)最後從原始的輸入陣列找到兩個值的位址

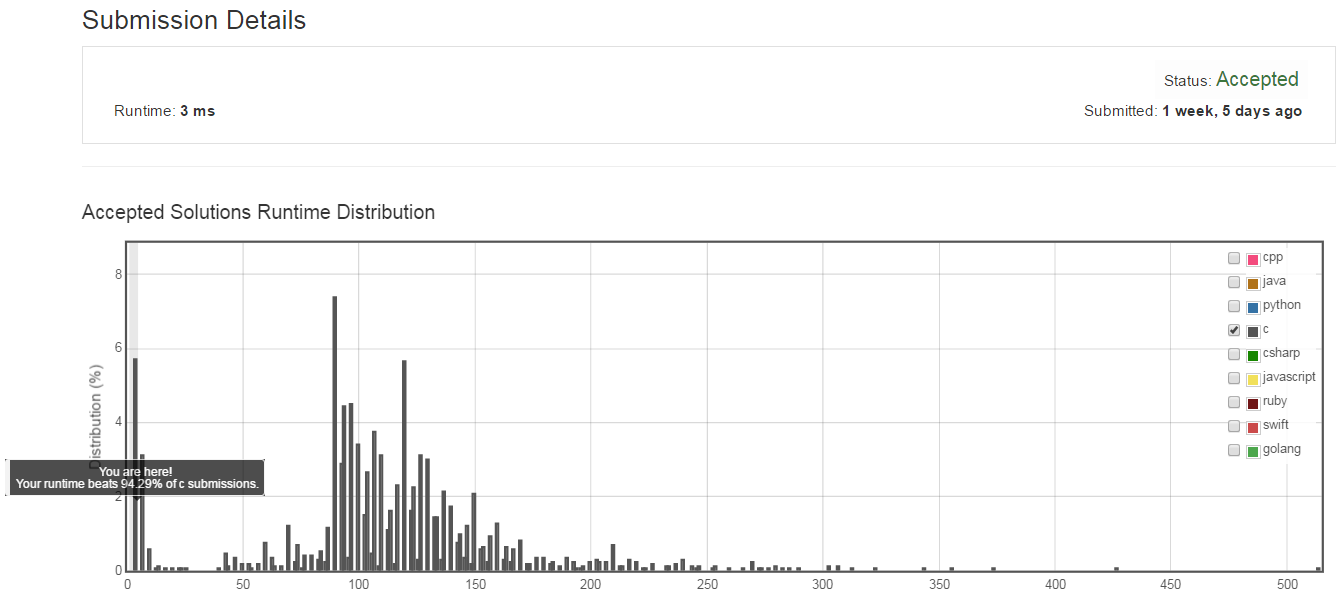
放到leet code上執行的結果為3ms明顯低於暴力解方式和binary search速度相當，超過94.29%的上傳程式